




0、2、5、7、8這五個數字各用一次,可以組成很多種五位數;
請找出其中的兩個五位數,且這兩個數相減的差為66942。
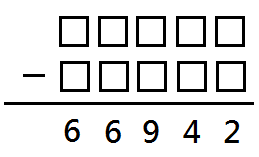
87520-20578=66942


為方便說明,將式子用下面代號表示:
ABCDE
-abcde
------------------
66942
首先決定最大位數A及a,兩數相減是6,有可能 A-a=6 或有被借一位 (A-1)-a=6,
所以要找0、2、5、7、8裡兩個數字相差6或相差7的,
只有兩種可能:(8,2)跟(7,0),其中0不能當最大位數,所以A=8,a=2;
8BCDE
-2bcde
------------------
66942
同理,B跟b也是要找要找0、2、5、7、8裡兩個數字相差6或相差7的,
(8,2)已經被用掉了,所以只剩(7,0),B=7,b=0;
87CDE
-20cde
------------------
66942
已知C-c有向千位數借一位,所以 10+C-c=9 或也有被十位數借一位 10+(C-1)-c=9,
所以要找0、2、5、7、8裡兩個數字相差-1或相差0的,
相差-1的只有(7,8)這一組,但7已經被用過了,所以不合,
只能找兩個一樣的數字,
也因為前面用過0, 2, 7, 8,C跟c不能是這四個數字,只剩下C=c=5,
875DE
-205de
------------------
66942
接下來看個位數,E-e=2 或有跟十位數借一位 10+E-e=2,
要找0、2、5、7、8裡兩個數字相差2或-8的,有(7,5)跟(0,8),
其中第一個數字已經用過7了,所以只剩(0,-8),E=0, e=8,
875D0
-205d8
------------------
66942
剩下的D跟d就是剩餘的兩個數字啦:D=2, d=7

