




將數字1~9分別填入下面方格中(數字不能重複),使等式成立,
這次題目不像昨天已經幫你填好三格,
你可以找出除了昨天的答案之外的另一組答案嗎?
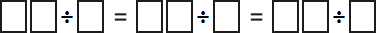
(註:等式算出來的結果也是一個整數)
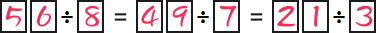


題目規定1~9只能各用一次,
所以數字5一定得填在十位數(不然就得重複用到5才有可能讓等式成立),
接下來解十位數是5的那個數字的個位數,
53跟59是質數,不能形成除式,昨天式子用過的54也不可能,
所以只可能是51, 52, 56, 57, 58這五個數字之一,
要知道是這五個中的哪一個數字,就要把除數也考慮進去,
除數是一位數,且不能是1(否則後面兩個等式的被除數就會超過100了),所以除數必須為2~9中的一個數字,
51在2~9之間的因數只有3,所以只能寫成51/3=17,
列出值為17的其他可能等式,又還沒有用過(1, 3, 5)的只有:68/4,
無法形成剩下兩個等式,所以不是51,
用同樣方法驗證其他四個數字,就可以找出只有56/8=7這個式子符合,
列出值為7的其他可能等式,又還沒有用過(5, 6, 8)的有:14/2, 21/3, 49/7,
從這三個式子中要選兩個出來,剛好用到(1, 2, 3, 4, 7, 9)的就是49/7跟21/3了

