




有黃、藍、朱三對夫妻一起圍著圓桌吃飯,他們一開始的座位是這樣的:
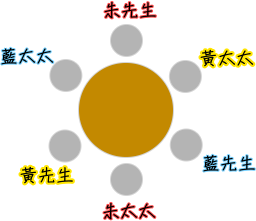
中途,有一半的人換了座位,另一半人沒換座位,新的座位是這樣的:
請問,這六個人後來到底是怎麼坐的呢?
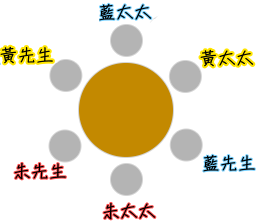


直接從新座位的條件(ii)(iii)可推知:藍先生兩側坐的是黃太太跟朱太太,
再配合條件(i)跟(iii),可推出:不管座位的方位,從藍先生開始往旁邊依序為:黃太太、藍太太、黃先生、朱先生、朱太太。
藍太太跟藍先生原先是坐對面,後來變成隔一個,所以藍姓夫婦兩人必定只有一個沒換位置或兩人都有換位置;
同理,黃姓夫婦也是只有一個沒換位置或兩人都有換位置;朱姓夫婦也是只有一個沒換位置或兩人都有換位置;
由於有三個人換座位,所以必定為每姓夫婦各有一個換坐位,另一個沒換,
所以只可能有2×2×2=8種換座位的假設組合,而不用把六個人中選三個的所有組合都假設過,
接下來再將這8種假設比對一下,
很容易就可以比對出來只有朱太太,藍先生、黃太太這三個人能同時滿足沒換座位的條件囉!

