




底下是一張4x4的黑白相間的紙板,
可以將相鄰的六個方格剪下,並翻摺做成立方體。
請問,使用這張紙板可以做出幾種外觀相異的立方體?
(隙縫可忽略,只要旋轉後發現配色一樣就算相同)

◎本題引用自遊戲學校,網友bbbnnn提供
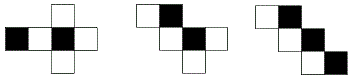
6種,在此為每種方塊列舉一種展開圖,
實際上每種方塊有多種切法,相信大家能夠自行比對:
經過仔細計算(M無誤),對應的立方體分別有

16種/8種/64種
 種/8種/8種(切法)
種/8種/8種(切法)
另外耀羽的問題2&3分別是30&120


題目的要求是「拼成立方體後顏色組合不同」,而顏色組合可分為六類:
(1) 6面同色
明顯地,只有一種顏色的話根本連接不起來。故不存在。
(2) 5面同色
1個方塊最多接4個不同顏色的方塊,因此第5個無法相接。故不存在。
(3) 僅4面同色,其餘2面分離(於對面)
此情況成立,即為答案中的左邊兩個。
(4) 僅4面同色,其餘2面相鄰(於隔壁)
此情況成立,即為答案中的中間兩個。
(5) 雙色各3面,且3面緊鄰
此情況成立,即為答案中右下角的那一個。
(6) 雙色各3面,且其中2面分離
此情況成立,即為答案中右上角的那一個。
值得注意的是3、4各有兩種解(黑白互換),而5、6顏色互換仍為一樣的立方體。
至於怎麼找呢?原理很簡單。
題目給的方格是黑白交錯,因此在展開立方體的時候,盡量將所有同樣顏色的方塊分離,
以此原則慢慢拆,應該不難拆出組合。

