




請把數字 1 ~ 9 不重複的填入下面的圓圈中,
讓三邊各自的數字總和都相等。
其中幾個圓圈已經幫你填好了:
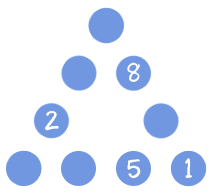
(提示:不要一開始就列成有好多未知數的等式來解,
想想有沒有比較快的解題方法吧!)
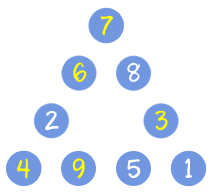


如果把三個邊的總和再相加在一起,就等於(1+2+3+4+5+6+7+8+9)+三個角落的數字,
既然三邊總和相等,所以這個值必定是 3 的倍數,
也就是三個角落的數字總和必定是 3 的倍數。
有一個角落已知是 1 ,剩餘還沒填入的數字有(3, 4, 6, 7, 9),
其中只有(4, 7)能符合 1+4+7=12 為 3 的倍數,
所以知道剩餘兩個角落分別為 4 跟 7;
也可得知單一個邊的總和就是[(1+2+3+4+5+6+7+8+9)+1+4+7]/3=19。
把各個圓圈標上符號方便說明:
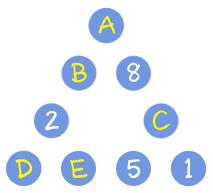
先看左邊:A+B+2+D=19
因為A, D兩個角落已經知道是 4 跟 7,總和 11
→ B=6
再看下面:D+E+5+1=19
而且E只可能是還沒確定的(3, 9)其中一個,
如果E=3,D就=10,與題意不合,
→E=9, D=4
剩下就可以解出 A=7, C=3 啦!

