




6x6方陣裡面已擺了12顆南瓜,
請移動其中的3顆,讓每個橫行、直列、對角線上都有2顆南瓜:
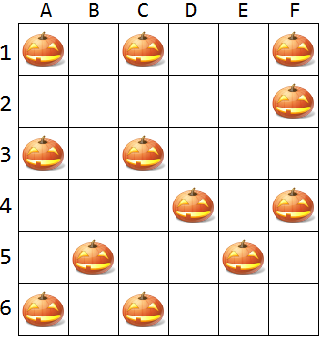
有兩種解:
把1A、1F、3C的南瓜移到1E、2D、3B(或者1B、2D、3E)即可。
如:
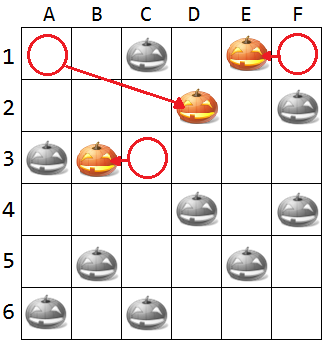


方陣總共有14條線(6橫、6直、2斜),
每條線都要數2個南瓜,所以總共會數2x14=28個南瓜;
南瓜如果放在對角線上,就會在橫直斜3條線上各被數一次,
如果不是放在對角線上,就會在橫直2條線上各被數一次,
也就是每顆南瓜基本會被數2次,若放在對角線上會再多數1次;
方陣裡有12顆南瓜,基本會被數24次,
要數28次的話就要有4顆南瓜放在對角線上,
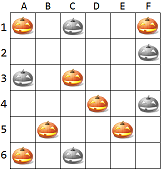
方陣裡的對角線已經有7顆南瓜,所以要移掉的3顆就是要從對角線中移掉,
也就是下圖中灰色南瓜不能動,要從橘色南瓜中選3顆移動:
(一) F列上已有三顆,一定要移掉一顆,只能選1F
(二) C列上已有三顆,一定要移掉一顆,只能選3C
(三) A列上已有三顆,一定要移掉一顆,可以移1A或6A
(四) 左上到右下的對角線上移掉3C後仍有三顆,可以移1A或4D或5E
已經移掉1F跟3C了,只能再移掉一顆,要讓第(三)(四)點都有被移掉一顆,就只能選1A了;
把1F、3C、1A三顆移出來後,接下來要決定把它們移到哪裡,
把已經滿兩顆不能再放南瓜的格子打叉:
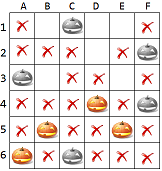
第2行少一顆,一定得放在2D,
剩下1B、3B、1E、3E四格要放兩顆,
要交錯放,所以1E+3B或1B+3E這兩種放法都是可以的;
所以答案就是把1A、1F、3C的南瓜移到2D、1E、3B 或者 2D、1B、3E。

