




請把1, 7, 13, 31, 37, 43, 61, 67, 73這九個質數填入下面的九宮格中,
使每一直、橫、斜行的數字總和是相等的。
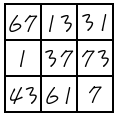
(左右對調或順逆時鐘90o旋轉幾次,都是正確的)


先觀察下面這四條紅線連起來的直橫斜行,
正中間的格子是四條線都會用到的,所以A+B=C+D=E+F=G+H,
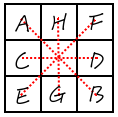
也就是要在這九個質數裡面,挑出一個放在正中間,其餘八個兩兩相加會相等。
可寫成:(1+7+13+31+37+43+61+67+73)-中間格子的數=4的倍數
觀察這九個數字的個位數,三個是1, 三個是3, 三個是7,
若要產生出兩兩相加相等的四組數,那麼四組數的個位數只能是(1, 3), (1, 3), (1, 3), (7, 7)
也就是剩下要被放在中間格子的數字個位數一定是7;
把7, 37, 67分別代進333-中間格子=4的倍數的式子裡,會發現只有37符合,
所以中間格子就是37,A+B=C+D=E+F=G+H=(333-37)/4=74,
四組數字分別是(1, 73), (13, 61), (31, 43), (7, 67);
先從數字最極端的(1, 73)這組來判斷要放在哪個位置,
因為九宮格可以任意90o旋轉數次或左右對調不改變每行的和,
可能的位置就只有兩種:斜角(如AB)或直橫線(如CD);
看下面這四行不會經過中間格子的連線,它們的和也要等於74+37=111,
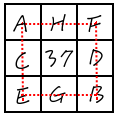
如果(1,73)放在斜角(A, B),則D+F=E+G=111-73=38,
但剩餘的7, 13, 31, 37, 43, 67, 61這七個數字裡無法找到兩組相加都是38的,
所以(1, 73)必須放在(C, D)這種直橫線上:
| A | H | F |
| 1 | 37 | 73 |
| E | G | B |
由B+F=111-73=38,(B, F)=(7, 31)
| A | H | 31 |
| 1 | 37 | 73 |
| E | G | 7 |
A=111-37-7=67 (斜線),剩下的E, H, G也很容易就推出來了。

