




把1~9各使用一次,填入下面的方格中,讓等式成立:
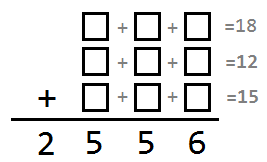
(三個三位數相加總=2556,每個三位數的各自數字和分別為18、12、15)
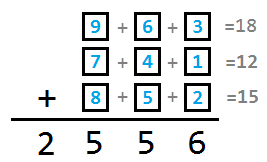


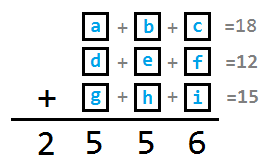
1~9中選三個數字之和的範圍在(1+2+3)~(7+8+9) → 6~24之間,
可知十位數(b+e+h)一定有進位1或2給百位數(a+d+g),
1~9的全部數字加起來是45,由於(a+d+g)>20,(b+e+h)>10,所以(c+f+i)只能是6
→ (b+e+h)=15,(a+d+g)=24
可以看到6跟24這兩個總和的極端值都出現了,所以:
個位數(c, f, i)一定是1, 2, 3(順序未知)
十位數(b, e, f)一定是4, 5, 6(順序未知)
百位數(a, d, g)一定是7, 8, 9(順序未知)
第一橫排,要從個、十、百位數的數組中各挑一個出來,總和為18,一定得挑各自最大的(3, 6, 9),
第二橫排一定得挑各自最小的(1, 4, 7),
答案就全部出來啦!

