




a、b、c、d、e代表不同的數
且abcde x 4 = edcba (註:abcde代表a萬b千c百d十e...,非相乘。)
請問a、b、c、d、e各是多少呢?
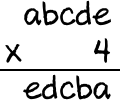
◎本題引用自遊戲學校,網友ms0592138提供
abcde=21978
→21978x4=87912


用直式思考:
abcde
x 4
----------
edcba
先看最高位數,abcdex4仍為5位數
→ax4不可超過10
→a=1 or 2
接著看個位數,ex4尾數為a,代表a不能是奇數
→所以a=2
代回式子中:2x4=8,且8x4=32,恰好符合上下式的a和e,
→所以e=8,也可知道前一位的bx4沒有進位
由前面得知的bx4=d沒有進位→bx4不可超過10
→b=1 or 2
而2已經被a用掉了→b只能是1
把以上資訊再寫回式子中:
3
21cd8
x 4
----------
8dc12
看十位數,4xd再+3會得到尾數1,代表4xd的尾數是8,
→d=2 or 7
但2已經被a用掉,所以d=7,
十位數算出來的結果是4x7+3=31,會進位3到百位數:
33
21c78
x 4
---------
87c12
剩下c,先看千位數的4x1竟然得到7,表示4xc也是進位3,
→4xc+3=30+c
→c=9
以上,就全部都解出來啦!

